Matematika Penerapan Kesebangunan

“ Penerapan Kesebangunan dalam Kehidupan Sehari-hari ”

Makalah ini Disusun Untuk Memenuhi Salah Satu Tugas Mata Kuliah

“ Matematika 3 ”

Disusun Oleh

Lutfatur Rodhika        (210613130)

Kelas : PG.D

Dosen Pengampu :

Kurnia Hidayati, M.Pd

PRODI PENDIDIKAN GURU MADRASAH IBTIDAIYAH

JURUSAN TARBIYAH

SEKOLAH TINGGI  AGAMA ISLAM NEGERI

(STAIN) PONOROGO

2014

KATA PENGANTAR

Assalamu’alaikum Wr. Wb

Segala puji bagi Allah Swt atas petunjuk dan kekuatan yang diberikan kepada saya untuk membuat makalah ini. Shalawat serta salam tetap terlimpahkan kepada junjungan kita yakni Nabi Muhammad Saw yang telah membawa umatnya menuju jaman sekarang ini.

Makalah ini diajukan sebagai tugas mata kuliah Matematika 3, Adapun judul makalah yaitu Penerapan Kesebangunan dalam Kehidupan Sehari-hari. Penulis menyadari banyak kekurangan dalam penyusunan makalah ini. Namun, Penulis berharap semoga makalah ini dapat bermanfaat bagi Penulis pada khususnya dan pembaca pada umumnya.

Wassalamualaikum Wr. Wb.            

Ponorogo, 21 Februari 2015  

                                Penulis

Daftar Isi

Kata pengantar……………………………………………………..…………... ii

Daftar isi……………………………………………………………………..….iii

BAB I PENDAHULUAN

   A.    Latar belakang………………………………………………………...........1

   B.     Rumusan masalah………………………………………………………......1

   C.     Tujuan……………………………………………………............................1

BAB II PEMBAHASAN

   A.    Penerapan kesebangunan bangun datar dalam kehidupan sehari-hari….......2

   B.     Penerapan kesebangunan segitiga dalam kehidupan sehari-hari……...........3

BAB III PENUTUP

Simpulan………………………………………………………………………….5

Daftar pustaka………………………………………………………………….…6

BAB I

PENDAHULUAN

  A.    Latar Belakang

Membandingkan dua benda secara geometris dapat dilihat dari dua aspek, yaitu bentuk dan ukurannya. Satu benda yang memiliki bentuk yang sama tapi dengan ukuran berbeda banyak dijumpai atau digunakan dalam kehidupan sehari-hari. Misalnya, miniatur bangunan dan bangunan itu sendiri, peta suatu daerah dengan daerah sesungguhnya dan lain-lain.

Dua benda yang memiliki bentuk yang sama tetapi ukurannya berbeda disebut sebangun. Adanya kesebangunan antara dua benda akan berguna untuk mengungkapkan informasi berkaitan dengan benda kedua dengan memanfaatkan informasi pada benda pertama atau sebaliknya.

Dalam, kehidupan sehari-hari, kita dapat menemukan bentuk-bentuk bangun datar dalam sebuah bangunan rumah. Misalnya jendela dan pintu berbentuk persegi panjang, lubang ventilasi berbentuk segitiga, dan ubin lantai berbentuk persegi.

  B.     Rumusan Masalah

1.      Bagaimana penerapan kesebangunan bangun datar dalam kehidupan sehari-hari ?

2.      Bagaimana penerapan kesebangunan segitiga dalam kehidupan sehari-hari ?

  C.    Tujuan

1.      Untuk mengetahui penerapan kesebangunan bangun datar dalam kehidupan sehari-hari.

2.      Untuk mengetahui penerapan kesebangunan segitiga dalam kehidupan sehari-hari.

BAB II

PEMBAHASAN

Penerapan Kesebangunan dalam Kehidupan Sehari-hari

Penerapan kesebangunan dalam kehidupan sehari-hari diantaranya adalah untuk penentuan jarak atau tinggi secara tidak langsung. Benda dapat dikatakan sebangun jika sudut-sudut yang bersesuaian besarnya sama dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama.[1]  Konsep dan sifat-sifat kesebangunan dapat digunakan untuk menyelesaikan masalah-masalah atau soal cerita yang berkaitan dengan kesebangunan. Untuk menyelesaikan soal cerita dapat dibantu dengan membuat sketsa atau gambar. Berikut ada beberapa penerapan kesebangunan pada bangun datar dan segitiga dalam kehidupan sehai-hari.[2]

A.  Penerapan kesebangunan bangun datar dalam kehidupan sehari-hari

1)   Andi menggambar lapangan sepakbola dengan panjang 4 cm dan lebar 3 cm. Jika panjang lapangan sepakbola yang sebenarnya 300 m, berapakah lebar lapangan sepakbola yang sebenarnya ?

Penyelesaian :

Bandingkanlah panjang lapangan sepakbola sebenarnya (Gambar b) dengan panjang lapangan sepakbola pada gambar (Gambar a). Lakukan pula pada lebar lapangan sepakbola sebenarnya dengan lebar lapangan sepakbola pada gambar, ubahlah satuannya sehingga sama. Panjang lapangan sepakbola yang sebenarnya 300 m = 30000 cm.

    l     = 30000 cm
3 cm         4 cm

l x 4 cm= 3 cm x 30000 cm

l = 90000 cm
        4 cm

l = 22500 cm = 225 m

Jadi, lebar lapangan sepakbola yang sebenarnya adalah 225 m. [3] 

B.     Penerapan Kesebangunan Segitiga dalam kehidupan sehari-hari

1)      Pada siang hari yang cerah, satu regu pramuka mendapat tugas menghitung tinggi sebuah tiang tanpa harus memanjat. Mula-mula diambil sebatang tongkat yang panjangnya 160 cm, kemudian tongkat tersebut didirikan tegak lurus di atas tanah rata. Anggota pramuka yang lain menghitung panjang bayangan tiang dan panjang bayangan tongkat. Ternyata, panjang bayangan tiang 375 cm dan panjang bayangan tongkat 80 cm. tentukan tinggi tiang !

Penyelesaian :

Tinggi tiang h, dan bayangannya 375 cm, sedangkan tinggi tongkat 160 cm dan bayangannya 80 cm. karena kedua segitiga di atas adalah sebangun, sisi bersesuaian sebanding, maka diperoleh :

     h      =  375 cm

160 cm      80 cm

h = 160 cm x 375 cm

                80 cm

h = 60.000 cm

          80 cm

h = 750 cm

Jadi, tinggi tiang adalah 750 cm.

2)      Untuk menentukan lebar sungai yang arusnya deras, satu regu pramuka telah menyelesaikan sketsa seperti gambar di bawah ini.

Tentukan lebar sungai !

Penyelesaian :

Misalnya lebar sungai h m

Perhatikan bahwa ∆ ABE ≈ ∆ CDE dan sisi bersesuaian sebanding, sudut-sudutnya sama besar sehingga

EC = CD

EA    AB

EC = EA CD

                AB

h = (h +3 m) 4 m
                    6 m

h = (h+3 m) 2 m
                   3 m

h = 2 m h + 2 m
      3 m

h - 2 m = 2 m
     3 m

1/3 h = 2 m

h = 6 m

Jadi, lebar sungai 6 m. [4]

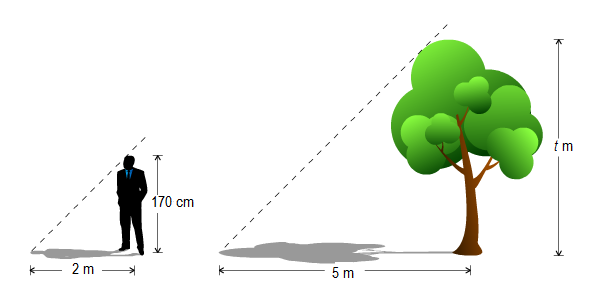
3)      Seorang pemuda yang tingginya 170 cm berdiri di samping pohon yang mempunyai bayangan 5 m. jika panjang bayangan pemuda itu 2 m, berapa tinggi pohon yang sebenarnya ?

Penyelesaian :
Diketahui :
tinggi pemuda = 170 cm = 1,7 m
bayangan pohon = 5 m
bayangan pemuda = 2 m
Ditanya : tinggi pohon  ?
Jawab :

    t    = 5 m

1,7 m   2 m

t = 1,7 cm x 5 cm

            2 cm

t = 4,25 m

jadi, tinggi pohon sebenarnya 4,25 m. [5]

BABA III

PENUTUP

Simpulan

Suatu benda dikatakan sebangun jika sudut-sudut yang bersesuaian besarnya sama dan sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Penerapannya banyak kita temukan dalam kehidupan sehari-hari, seperti mengukur tinggi tiang bendera, kita tidak perlu memanjat tiang bendera tersebut. Kita dapat mengukurnya dengan cara membandingkan dengan tongkat. Selain itu mengukur lebar sungai, lebar lapangan sepakbola. Dalam kehidupan sehari-hari, kita juga banyak  menemukan bentuk-bentuk bangun datar dalam sebuah bangunan rumah. Misalnya jendela dan pintu berbentuk persegi panjang, lubang ventilasi berbentuk segitiga, dan ubin lantai berbentuk persegi.

DAFTAR PUSTAKA

http://dualmode.kemenag.go.id/file/dokumen/MTK6.pdf

http://workshopmathematics.blogspot.com/2012/12/bab-1-kesebangunan-dan-kekongruenan.html

Modul PGMI Matematika 3

Riduan dkk. Modul Bahan Ajar Matematika Kelas 9. Madiun: Anugerah Agung, 2014

---

[1] Modul PGMI Matematika 3, 4-20

[2] http://workshopmathematics.blogspot.com/2012/12/bab-1-kesebangunan-dan-kekongruenan.html

[3] http://dualmode.kemenag.go.id/file/dokumen/MTK6.pdf

[4] Modul PGMI Matematika 3, 4.20-4.21

[5]Riduan dkk, Modul Bahan Ajar Matematika Kelas 9, (Ponorogo: Anugerah Agung, 2014), 11